-
-
\( f(x) = \sqrt{x-1}\) の $x=4$ における微分係数
$x=4$ における微分係数は
-
\begin{align}f'(4) = \lim_{\Delta x\rightarrow 0} \frac{f( 4+{\Delta x} ) - f(4)}{\Delta x}\end{align}
-
\( f( x ) = \sqrt{x-1 \ } \) の式中の $x$ は「記入欄」だと思って
\( f( ) = \sqrt{( )-1 \quad } \) と書き、
\(x = 4+{\Delta x} \) なら ( ) に \(4+\Delta x \) をかいて
\( f( 4+{\Delta x} ) = \sqrt{(4+{\Delta x})-1 \ } \)
これを最初の式に代入していきます
$x=4$ における微分係数
-
\begin{align}f'(4)
&=& \lim_{\Delta x\rightarrow 0} \frac{f( 4+{\Delta x} ) - f(4) }{\Delta x}
\\
\\
&=& \lim_{\Delta x\rightarrow 0} \frac{ \sqrt{ 4+{\Delta x}-1 \ } - \sqrt{ 4 -1 } }{\Delta x}
\\
\\
&=& \lim_{\Delta x\rightarrow 0} \frac{ \sqrt{ 3+ {\Delta x} \ } - \sqrt{ 3 } }{\Delta x}
\end{align}
ルートのついた数どうしは
そのままでは引き算できないので
引き算できるようにするために
ルートを外さないといけません。
ルート外すためには2乗する必要があります。
前も2乗、後ろも2乗。
$a^2-b^2 = (a-b)(a+b) $
\(\sqrt{ 3+ \Delta x}\) を$a$、\(\sqrt{3}\) を$b$ と思ってこれを使いましょう。
上下に
\( ( \sqrt{ 3+ {\Delta x} \ } + \sqrt{ 3 }) \)をかけて
\begin{align}f'(4)
&=& \lim_{\Delta x\rightarrow 0}
\frac
{ (\sqrt{ 3+ {\Delta x} \ } - \sqrt{ 3 })\cdot
( \sqrt{ 3+ {\Delta x} \ } + \sqrt{ 3 }) }
{\ \Delta x \cdot
\ ( \sqrt{ 3+ {\Delta x} \ } + \sqrt{ 3 })}
\\
\\
&=& \lim_{\Delta x\rightarrow 0}
\frac
{ \sqrt{ 3+ {\Delta x} \ }^2 - \sqrt{ 3 }^2 }
{\ \Delta x \cdot
( \sqrt{ 3+ {\Delta x} \ } + \sqrt{ 3 }) \quad }\quad
\\
\\
&=& \lim_{\Delta x\rightarrow 0}
\frac
{ 3+ {\Delta x} - 3 }
{\ \Delta x \cdot
( \sqrt{ 3+ {\Delta x} \ } + \sqrt{ 3 }) \quad }\quad
\\
\\
&=& \lim_{\Delta x\rightarrow 0}
\frac
{ \Delta x }
{\ \Delta x \cdot
( \sqrt{ 3+ {\Delta x} \ } + \sqrt{ 3 }) \quad }\quad
\\
\\
&=& \lim_{\Delta x\rightarrow 0}
\frac
{ 1 }
{\ 1 \cdot
( \sqrt{ 3+ {\Delta x} \ } + \sqrt{ 3 }) \quad }\quad
\\
\\
&=& \frac
{ 1 }
{\
( \sqrt{ 3+0 } + \sqrt{ 3 }) \quad }\quad
\\
\\
&=& \frac
{ 1 }
{\ 2 \ \sqrt{ 3 }\quad }\quad
\\
\\
\end{align}
x=4 における微分係数、すなわち増加率は、
横に$ 2 \ \sqrt{ 3 }$ 行って 縦に 1 上がる、くらいの傾き。どうでしょう
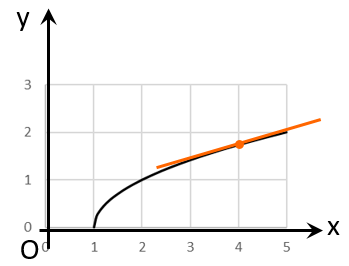
よさそうですね
次へ
|
