-
これまで求めてきた導関数
-
\begin{align}f'(x)
= \lim_{\Delta x\rightarrow 0} \frac{f( x+{\Delta x} ) - f(x)}{\Delta x}
\end{align}
は、
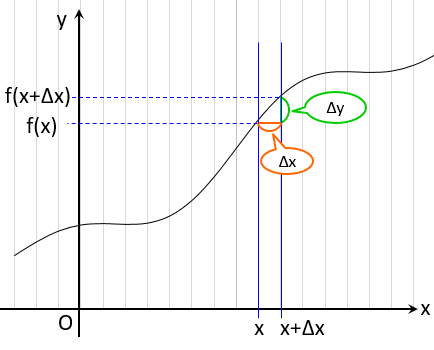
「 $x$ から $x+{\Delta x}$ にかけての増加率
$\displaystyle {\Delta y \over \Delta x}$ を詳しくしたもの」でした。
\begin{align}f'(x)
= \lim_{\Delta x\rightarrow 0} \frac{ \Delta y }{\Delta x}
\end{align}
${\Delta x}$ は $x$ の増えた分(増分)、
${\Delta y}$ は $y$ の増えた分です。
この式は、
$\displaystyle \lim_{\Delta x\rightarrow 0}$ を使わないで書くと、このようにも書けます。
\begin{align}
\frac{\Delta y}{\Delta x} \rightarrow f'(x)
\qquad({\Delta x \rightarrow 0} のとき)
\end{align}
この式の両辺に $\Delta x$ をかけるとこうなります。
\begin{align}
\Delta y \rightarrow f'(x) {\Delta x}
\qquad({\Delta x \rightarrow 0} のとき)
\end{align}
つまり、上の図の $\Delta y$ は、$f'(x)$ と $\Delta x$ でわかるということですね。
さて、この $\Delta y$ は、$x$から $x+{\Delta x}$ までの区間の $y$ の増分でしたが、
この前の区間とか、これの次の区間とかについても、
同じように $y$ の増分$\Delta y$ を求めることができます。
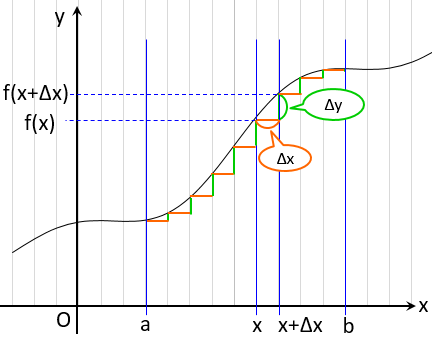
これを、$x=a$ から $x=b$ までのたくさんの区間について
全部足し算したらどうでしょう?すこしづつ増えた $\Delta y$を
全部積み重ねていくことになります。
ちなみに 「$x=a$ から $x=b$ までについて全部足す」
を表す記号が $\displaystyle \sum_{x=aから}^{x=bまで}$ です。「総和」ともいいます。
英語で言うとsum(合計) です。頭文字 S です。
英文字の Sに対応するギリシア文字が $\Sigma$ です。シグマと呼んでます。
\begin{align}
\sum_{x=aから}^{x=bまで} \Delta y
\rightarrow
\sum_{x=aから}^{x=bまで} f'(x) {\Delta x} \quad
\qquad({\Delta x \rightarrow 0} のとき)
\end{align}
$\Delta y $ の総和は、
$f'(x) {\Delta x} $ の総和に近づくってこどです。
次の図を見て分かる通り、$\Delta y $ の総和は、$f(b)-f(a)$ になりますね。
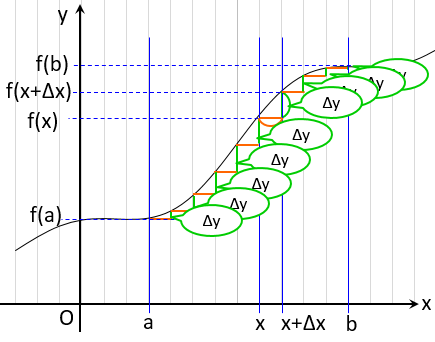
よって
\begin{align}
\sum_{x=aから}^{x=bまで} f'(x) {\Delta x} \quad
\rightarrow
f(b) - f(a)
\qquad({\Delta x \rightarrow 0} のとき)
\end{align}
ここで注目は${\Delta x \rightarrow 0}$ です。
$\Delta x$ を無限に細かくしています。
ただ足すだけでなく、$\Delta x$ を無限に細かく分けて足すとき、
ギリシア文字$\Delta $ を英語の d に替えて$\Delta x$ を $dx$ と書き、
ギリシア文字$\Sigma$ を英語の S を縦に引っ張った形に替えて
$\displaystyle \sum_{x=aから}^{x=bまで} $ を
$\displaystyle \int_{x=aから}^{x=bまで} $ と書きます。
これを使ったらもう
${\Delta x \rightarrow 0}$ は書かなくていいです。
よって
\begin{align}
\int_{x=aから}^{x=bまで} f'(x) \ dx \quad
=
f(b) - f(a)
\end{align}
これを $f'(x)$ の定積分と言います。
$f'(x)dx$ をちょっとずつ足していくと $f(a)$ から $f(b)$ まで増える
ということを表しています。
左辺の中身 $f'(x)$ は導関数ですね。微分してあります。
一方、右辺は $'$ がついておらず、微分前の元の関数 $f(x)$ です。
しかも最初の $x=a$ における値と最後の $x=b$ における値の差です。
右辺は、$ f(b) - f(a) $ と同じ式 $f$ を2回書くのは面倒なので
これを
$\Bigl[ \ f(x) \ \Bigr] _{x=aから}^{x=bまで}$ と書いてもいいことになっています。
$\Bigl[ \ f(x) \ \Bigr] _{x=aから}^{x=bまで} = f(b)- f(a)$ です。
終着点 $x=b$ の値を代入した式から、
出発点 $x=a$ を代入した式の引き算を表します。
これを使うと
\begin{align}
\int_{x=aから}^{x=bまで} f'(x) \ dx \quad
= \quad
\Bigl[ \ f(x) \ \Bigr] _{x=aから}^{x=bまで}
\end{align}
と書くことができます。
以上まとめると
\begin{align}
\int_{x=aから}^{x=bまで} (微分後) \ dx \quad
= \quad
\Bigl[ 微分前 \Bigr]_{x=aから}^{x=bまで}
\end{align}
- 使用例
-
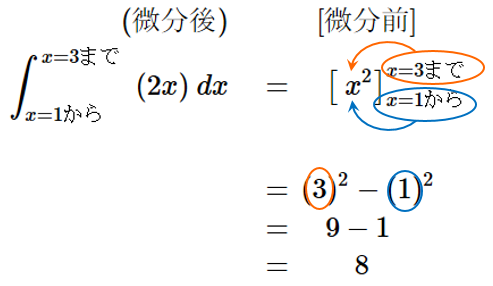
答えが数字になりましたね。このように、$x=$出発点 と$x=$終着点 が
指定されている定積分の答えは、式ではなく数字になります。
- 積分記号をノートに書くときは
- 積分記号や、代入のための\Bigl[ \Bigr] は「大型記号」といい、必ず2行使って書くのが決まりです。
2行使って書いたら、間を1行あけて、次にまた2行使って書いていきます。

- 高校では$x=$と書かなかった
-
高校で積分をやった方は、
\begin{align}
\int_{x=1から}^{x=3まで}(2x) \ dx \,
&= \, \Bigl[ \ x^2 \Bigr] _{x=1から}^{x=3まで}
\end{align}
とは書かずに、$x=$など付けないで
\begin{align}
\int_{1}^{3}(2x) \ dx \,
&= \, \Bigl[ \ x^2 \Bigr] _{1}^{3}
\end{align}
と書いていたと思います。
高校の時は、1変数関数しか扱わないので、
$x$ だけとか $t$ だけしか出てこないから困らなかったのですが、
大学では
\begin{align}
\int_{z=-d}^{z=d} \,
\int_{y=0}^{y=1} \,
\int_{x=-1}^{x=1} \,
f(x,y,z) \ dx \ dy \ dz
\end{align}
とか
\begin{align}
\int_{r=0}^{\infty} \,
\int_{\theta = -{\pi \over 2}}^{\theta = -{\pi \over 2}} \,
\int_{\phi=0}^{\phi = 2\pi} \,
f( r, \phi, \theta) \ dr , d\phi, d\theta
\end{align}
のように、多変数の積分を行うようになりますので、
どれにどれを代入するのか混乱しがちです。
1年前期では困らないのですが、今後の勉強での混乱を避けるために、
$x=$ を書いておくことをお勧めします。
(ただし$\infty$の時はイコールを書かないこと)
早速使ってみよう
|




