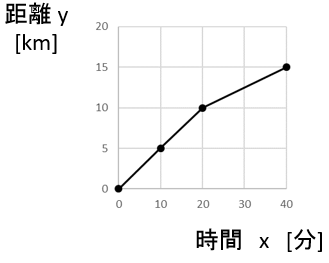
途中で折れる関数の例
時間 0 分に 0 [km]
時間 10 分に 5 [km]
時間 20 分に 10 [km]
時間 40 分でやっと 15 [km]
出だしの 0分から10分まで、とか、10分から20分まで、とかは
\(\Delta x \) = 20分 $-$ 10分 = 10分
\(\Delta y \) = 10km $-$ 5km = 5km
なので、増加率はさっきと同じ
\begin{align}増加率 \frac{\Delta y}{\Delta x} = \frac{5 [km]}{10 [分]} = 0.5 [km/分]\end{align}
ですが、後半ちょっと変わってきました。
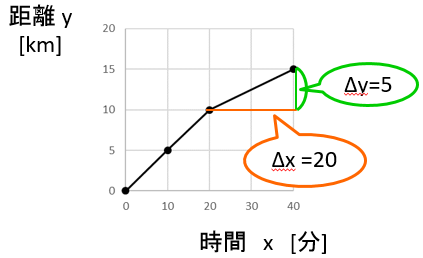
20分から40分までのところを見ると
\(\Delta x \) = 40分 $-$ 20分 = 20分
\(\Delta y \) = 15km $-$ 10km = 5km なので、増加率は
\begin{align}増加率 \frac{\Delta y}{\Delta x} = \frac{5 [km]}{20 [分]} = 0.25 [km/分]\end{align}
前より遅くなってます。
ちなみに、 20分から30分までの10分間だけ見ても
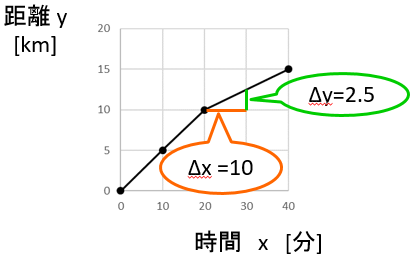
\(\Delta x \) = 40分 $-$ 30分 = 10分
\(\Delta y \) = 15km $-$ 12.5km = 2.5km なので、増加率は
\begin{align}増加率 \frac{\Delta y}{\Delta x} = \frac{2.5 [km]}{10 [分]} = 0.25 [km/分]\end{align}
やっぱり 0.25 [km/分]ですね。
ということはこのグラフは、前半と後半で増加率が変わっているということですね。
ではその増加率のグラフを、元のグラフと上下に並べて書いてみましょう。
次のページ