| 離散フーリエ変換(DFT) |
| 前のページから続く フーリエ級数展開 |
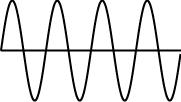
周期 T で繰り返す周期関数 f(x)
  のフーリエ級数展開は
のフーリエ級数展開はf(x)〜a0 + a1 cos(2px/T) + a2 cos(4px/T) + a3 cos(6px/T) + ... + am cos(2pmx/T) + ... + b1 sin(2px/T) + b2 sin(4px/T) + b3 sin(6px/T) + ... + bm sin(2pmx/T) + ... です。 a0 , a1 , a2 , ... をうまく選ぶと、元の波形を再現できるのでは、と思われます。 |
||||||||||||||||||||||||||||||||||||
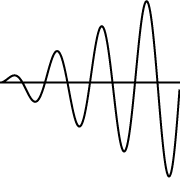
| 元の波形f(x)が 式で 与えられている時 |
ここに出てくる係数は a0 = (1/T) ∫0T f(x) dx am = (2/T) ∫0T f(x) cos(2mpx/T)dx bm = (2/T) ∫0T f(x) sin(2mpx/T)dx で求められます。
|
||||||||||||||||||||||||||||||||||||
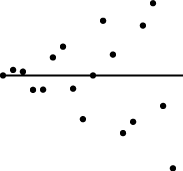
| f(x)が式でなく データで 与えられている時 |
f(x)が式でなくd秒間隔のデータで与えられている時は、
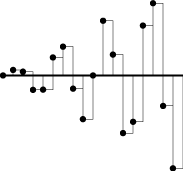
これじゃ積分できないので、定積分=面積 を思い出し、長方形の積分の和で代用しましょう。
a0 を求めるには fk (kは0, 1, 2, ...) の値をk=0 から k=N-1まで全部足して(1/N) をかければよく、 am を求めるには fk の値にcos(2mpk/N) をかけたものを全部足して(2/N) をかければよく、 bm を求めるには fk の値にsin(2mpk/N) をかけたものを全部足して(2/N) をかければよい、 ということになります。これならプログラムできそう。 |
||||||||||||||||||||||||||||||||||||
|
|
Σがピンとこない 手動でやってみる(4個) 手動でやってみる(8個) プログラムへ |